The graphical methods for checking data normality in R still leave much to your own interpretation. There’s much discussion in the statistical world about the meaning of these plots and what can be seen as normal.

Shapiro-Wilk Original Test. Note that if n is odd, the median data value is not used in the calculation of b. Calculate the test statistic W = b2 ⁄ SS Find the value in the Table 2 of the Shapiro-Wilk Tables (for a given value of n) that is closest to W, interpolating if necessary. This is the p-value for the test. An extension of Shapiro and Wilk's (W ) test for normality to large samples. Applied Statistics, 31, 115-124. Patrick Royston (1982). Algorithm AS 181: The (W ) test for Normality. Applied Statistics, 31, 176-180. Patrick Royston (1995). Remark AS R94: A remark on Algorithm AS 181: The (W ) test for normality.

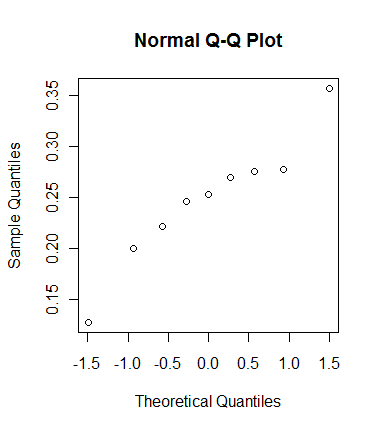
If you show any of these plots to ten different statisticians, you can get ten different answers. That’s quite an achievement when you expect a simple yes or no, but statisticians don’t do simple answers.

On the contrary, everything in statistics revolves around measuring uncertainty. This uncertainty is summarized in a probability — often called a p-value — and to calculate this probability, you need a formal test.

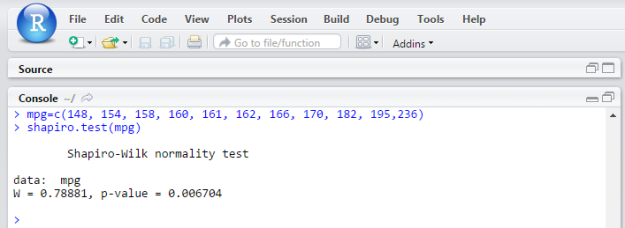
Probably the most widely used test for normality is the Shapiro-Wilks test. The function to perform this test, conveniently called shapiro.test(), couldn’t be easier to use. You give the sample as the one and only argument, as in the following example:

This function returns a list object, and the p-value is contained in a element called p.value. So, for example, you can extract the p-value simply by using the following code:

This p-value tells you what the chances are that the sample comes from a normal distribution. The lower this value, the smaller the chance. Statisticians typically use a value of 0.05 as a cutoff, so when the p-value is lower than 0.05, you can conclude that the sample deviates from normality.

In the preceding example, the p-value is clearly lower than 0.05 — and that shouldn’t come as a surprise; the distribution of the temperature shows two separate peaks. This is nothing like the bell curve of a normal distribution.

When you choose a test, you may be more interested in the normality in each sample. You can test both samples in one line using the tapply() function, like this:

This code returns the results of a Shapiro-Wilks test on the temperature for every group specified by the variable activ.

People often refer to the Kolmogorov-Smirnov test for testing normality. You carry out the test by using the ks.test() function in base R. But this R function is not suited to test deviation from normality; you can use it only to compare different distributions.